Staff/Rossi

· La ecuación logística y la evolución del COVID-19: los casos de Corea del Sur y México

· Ejercicio académico muestra consistencia entre estrategias gubernamentales y modelo matemático

Por: Dr. Alfredo Sandoval Villalbazo, académico del Departamento de Física y Matemáticas de la Universidad Iberoamericana Ciudad de México e Investigador Nacional Nivel II (SNI) / @Fred_FisMat

Es necesario advertir que el contenido de este artículo corresponde a un ejercicio académico que ilustra el funcionamiento de un modelo matemático de evolución de epidemias. No se pretende predecir formalmente aspectos relacionados con las posibles fechas del fin de la epidemia en México. Se busca, en cambio, promover la aplicación de contenidos de cursos universitarios en el análisis de eventos tales como la pandemia que afecta al planeta.

Durante las últimas semanas hemos escuchado que existen modelos matemáticos que permiten realizar, entre otras cosas, estimaciones respecto del número de infectados por el nuevo coronavirus. Uno de ellos corresponde a la llamada “ecuación logística”, en la cual el número de infectados “n(t)” al tiempo “t” satisface la ecuación diferencial [1-2 ] :

n'(t)= a n(t)+b (n(t))2 (1)

cuya solución general, obtenida por integración directa, es:

n(t)=1/(ⅇ^(-at) (1/n_o +b/a)-b/a) (2)

En estas ecuaciones a y b son constantes que se determinan a partir del número diario de casos comprobados, n0 es el número inicial de casos y ‘e’ es un número bien conocido en distintas áreas del conocimiento cuyo valor es aproximadamente 2.71828.

Para el caso de Corea del Sur, la ecuación (2) reproduce con precisión la llamada ‘curva epidémica de casos acumulados’ correspondiente al período del 19 de febrero al 25 de marzo del 2020. Esta curva, presente en la inmensa mayoría de las epidemias, adquiere una forma de ‘S’, y se conoce como función logística. La figura (1) muestra la función logística para el caso Surcoreano. Los valores calculados a partir de los datos disponibles hasta la primera semana de marzo corresponden a n0 =1 infectado, a=0.6443 días-1 y b=-0.000082 (infectados-día)-1 . Obsérvese que, partiendo de un valor cercano a cero, el número de infectados crece en una fase exponencial para posteriormente estabilizarse. Esto necesariamente tiene que ocurrir, dado que el número de infectados no puede exceder a la población total. Los casos acumulados diariamente siguen una curva en forma de campana y pueden obtenerse del modelo y de las medidas directas.

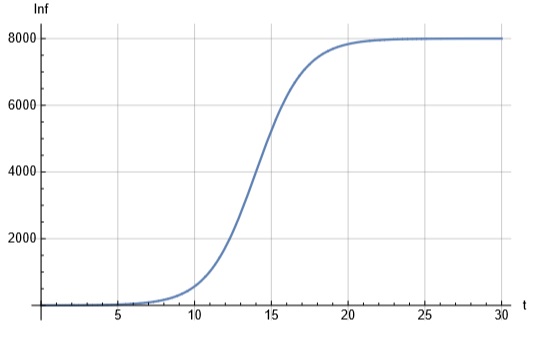
Para el caso de México es posible realizar un cálculo estimativo semejante que no debe entenderse como una predicción rigurosa, sino como un ejercicio académico relacionado con la contingencia actual. Dado que no se tiene la fecha exacta en la que se presentó el primer caso de COVID-19 en nuestro país, los valores numéricos incluidos en la ecuación logística únicamente serán ilustrativos. Si se considera que el 7 de abril se tuvieron 2785 casos verificados, que transcurrieron 42 días desde el primer caso hasta esa fecha y se consideran los casos verificados intermedios, los valores obtenidos son a=0.198835 días-1 y b=-0.00002447 (infectados-día)-1. El comportamiento de la función se muestra en la figura 2, en la cual se sugiere que la curva comenzará a estabilizarse a finales de abril y se estabilizará firmemente a principios de mayo, con cerca de 8200 casos verificados de infectados.

Todo modelo matemático debe ser tomado con precaución [3]. En particular, la ecuación logística es muy sensible al valor de los parámetros involucrados en ella, los cuales a su vez dependen de datos que pudieran involucrar incertidumbres significativas. Si, cuando comience la estabilización de la curva epidémica se perdiera la disciplina y se hiciera un regreso mal planeado a las labores, la fórmula obtenida perdería todo su valor. Adicionalmente, es importante recordar que el número de casos verificados de COVID-19 en México representa aproximadamente una octava parte de los casos reales, por lo que debe considerarse fundamentalmente la forma de la curva epidémica y no simplemente los valores numéricos. En cualquier caso, los cálculos mostrados invitan a realizar nuevos ejercicios académicos vinculados con la realidad nacional inmediata.